MPU 论文阅读笔记
论文:Patch-based Progressive 3D Point Set Upsampling
一、摘要及引言
点云通常是稀疏、嘈杂且不完整的,这意味着上采样技术非常重要,但将图像中的超分辨率方法迁移到点云中并不容易。PU-Net 通过多尺度学习及特征扩展的方式来扩大点集,但无论输入的几何结构是大规模的还是细粒度的,PU-Net 都将使用同样的尺度来处理,以致于其重建结果往往缺乏细粒度的几何结构。
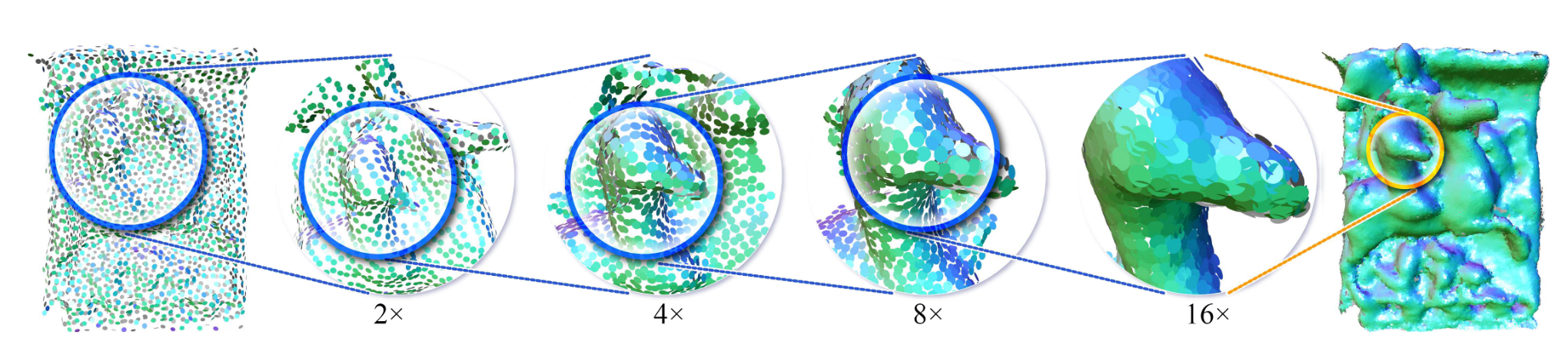
论文提出了一种 patch-based 渐进式上采样网络,将一个 $16\times$ 上采样网络分成四个 $2\times$ 网络,其中每个子网络侧重于不同级别的细节。
所有子网络都是完全基于 patch 的,并且输入 patch 的大小相对于当前的细节级别是自适应的。论文提出了一系列架构改进,包括用于逐点特征提取的新型密集连接、用于特征扩展的编码分配,以及用于层间特征传播的双边特征插值。这些都会在后面详细介绍。
二、相关工作
主要介绍了基于优化和基于深度学习的方法。论文指出了 PU-Net 对高分辨率输入效果较好,但缺乏细节;EC-Net 在锐利特征上有所加强,但边缘标记的工作量很大。论文还特别提到了深度学习中的多尺度 skip connection 方法,如 CNN 里的 U-Net 、ResNet 等。针对点云上采样问题,论文在不同组件中采用了不同的 skip connection 策略。
三、方法
多步上采样网络(Multi-step Upsampling Network)
多步监督(Multi-step Supervision)
Multi-step supervision 是神经图像超分辨率(neural image super-resolution)中的常见做法。简言之,对于上采样任务, Multi-step supervision 通常先将输入图像重建到一个中间分辨率,然后利用已知的高分辨率图像进行监督学习;之后再重建到更高的分辨率,再次进行学习。

这种做法的好处在于它允许模型在各个阶段学习和纠正错误,而不仅仅是在最终阶段。其次,它允许模型学习在不同分辨率之间的显式映射,这可能有助于使上采样结果更准确。
多步 patch-based 感受野(Multi-step patch-based receptive field)
理想情况下,点集上采样网络应针对各种细节尺度自适应地跨越感受野,以从多个尺度学习几何信息。然而不同于图像,点集没有规则结构,每个点的邻域都需要通过 $k$ 近邻的方式去查找,计算代价非常大,这使得多步上采样难以应用在点云中。因此有必要优化网络架构,使其可扩展到高分辨率点集。
论文应对这一问题的关键想法是:patch 大小应适应当前步骤的感受野范围。感受野的范围实际上由 $k$ 的大小决定,若 $k$ 固定,则随着点集不断被上采样,感受野会变小。因此论文提出的网络在上采样的同时,缩小了 patch 的空间跨度,减少了计算量。
由于需要对每个点做 KNN ,设总点数为 $N$ ,patch 大小为 $p_{num}$ ,其计算复杂度可以大约估算:
因此随着 patch 大小缩减,计算复杂度也会降低。
多步端到端训练(Multi-step end-to-end training)
网络通过 $L$ 步将点集上采样 $2^L$ 倍,包括子网络单元 $\{U_1,U_2,\dots,U_L\}$ 。论文通过逐步激活每个单元的方式来训练这一系列上采样单元。具体地,除了第一层网络,每一层网络的训练都包含两步:对于层次 $\hat{L}$ ,首先固定前面 $U_1$ 到 $U_{\hat{L}-1}$ 每一层的参数,只对 $U_{\hat{L}}$ 层训练;然后释放固定单元,对所有单元同时训练。
这种渐进式的训练方法是为了避免当前层产生过大的梯度(gradient turbulence),导致前面的单元参数被破坏。
上采样网络单元
分别用 $T,P,Q$ 表示基准模型、预测 patch 和 参考 patch ,$\hat{L},\ell$ 表示目标的细节级别和一个中间级别。简单来说,上采样网络单元 $U_{\ell}$ 首先接收来自于点集 $P_{\ell-1}$ 的 patch ,然后提取深度特征并扩展特征数量,将特征通道数压缩到 $d$ 维坐标 $P_{\ell}$ 。下面做详细说明。
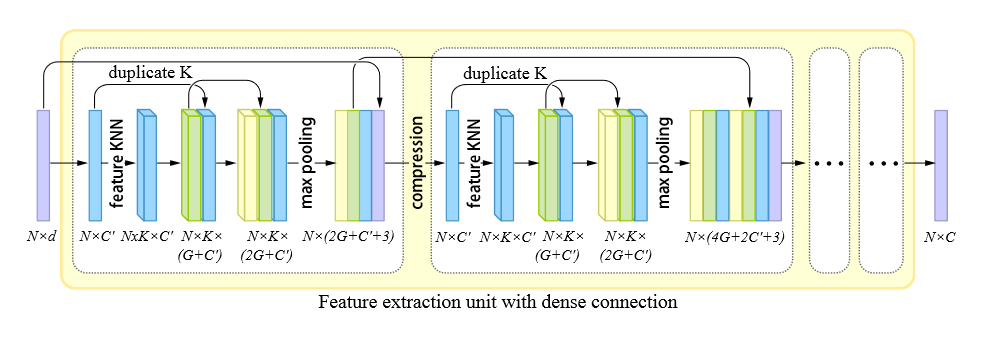
通过层内密集连接提取特征
在 PointNet++ 之后,大多数网络都采用对输入点集进行分层下采样的方式来提取多尺度信息,并采用 skip-connections 来连接多级特征。然而由于在下采样过程中采用了泊松盘采样或者最远点采样,导致点的位置发生变化,因此在特征连接的时候,需要进行点与点之间的对应搜索,导致计算代价增加。
收到 DGCNN 的启发,论文在特征空间中定义了局部邻域,因此网络无需点集子采样即可获得大范围、非局部的信息,也就不需要在特征组合时进行对应搜索。
如下图所示,论文的特征提取单元由一系列密集块(dense block)组成。在每个 dense block 中,首先将输入转换为固定维数 $(C’)$ 的特征,然后使用基于特征的 KNN 对特征进行分组,得到分组特征 $(N\times K\times C’)$ 。进而通过 MLP ,将特征重组为 $G’$ 维。实际上,在每个 dense block 内部,MLP 的输出维度都是固定的 $(G’)$ ,并且每经过一次特征处理,就会将上一步的特征拼接在后面,因此每一次处理都使得特征维数增加 $G’$ 。最后通过最大池化得到一个顺序不变的点特征。而在 dense blocks 之间,每个块产生的点特征会作为后面所有的 dense blocks 的输入(因为 dense block 的输出也会和上一个 block 的输出连接。相当于内部外部嵌套地进行 skip connections )。
这种 skip-connection 的方式能够复用显式信息,从而提高重建精度。同时相比于 PU-Net 在每一次下采样后用 PointNet 层聚合特征的方式,论文的特征提取方法能够显著减小模型参数量。
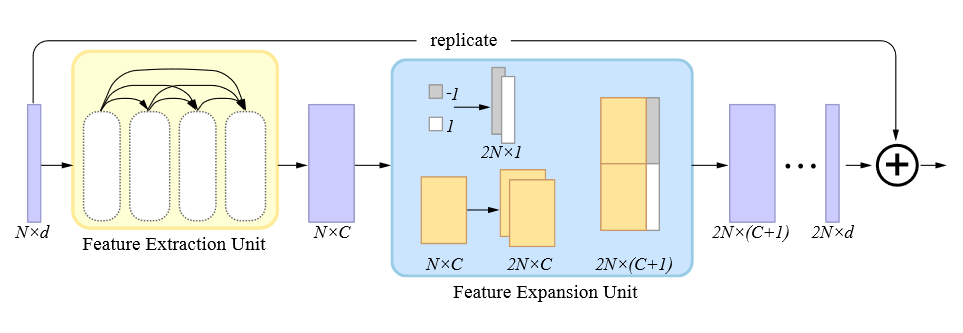
通过编码分配扩展特征
特征扩展单元的目标是将提取得到的特征 $(N\times C)$ 扩展为一组上采样的点坐标 $(2N\times d)$ 。PU-Net 的策略是复制每个点的特征,然后通过独立的 MLP 去处理所有的复制特征。但这会造成点的集中分布,PU-Net 通过添加了排斥损失来缓解这一问题。
论文借鉴了 FoldingNet 和 AtlasNet 。简单浏览了一下 FoldingNet ,大致思路是:首先从三维模型中提取了全局特征,然后复制一定数量,连接到一个二维网格点后面,将其重建为三维点,再次将复制后的全局特征连接到三维点后,重建成最终的具有预设数量的三维点。
论文的方法则更为简单,它将 $N$ 个 $-1$ 和 $N$ 个 $1$ 组成的一维张量拼接在复制了两份的特征向量后面(code assignment),再利用一系列共享的 MLP 将其压缩为 $2N\times d$ 的残差。将残差和原始坐标求和即得到新的上采样坐标,这与 EC-Net 的做法是一样的。区别于 PU-Net 和 EC-Net 在特征扩展部分所采用的策略,共享的 MLP 意味着参数量不会随着上采样率增大而增大(突然有个想法,如果后面接的特征不是 $1$ 和 $-1$ ,而是在 $4\pi$ 空间上均匀采样的 $2N$ 个方位角呢,会不会发散得更合理)。
通过双边特征插值实现层间 skip connection
上述两个组件已经实现了特征的嵌入和特征的扩展,这两者合在一起构成一个上采样单元。为了融合不同感受野提取的特征,论文在多个上采样单元之间使用了 skip connection 。由于点数增长,在连接之前需要进行特征插值。对于级别 $\ell$ ,$p_i$ 表示第 $i$ 个点坐标,$f_i$ 表示通过特征提取组件得到的该点特征。$\mathcal{N}_i’$ 表示第 $p_i$ 在级别 $\ell’$ 中的空间 KNN 近邻点集,则插值特征 $\widetilde{f}_i$ 表示为:
显然 $\theta$ 和 $\psi$ 是两个权重函数。其中 $\theta(p_1,p_2)=e^{-\left(\frac{|p_1-p_2|}{r}\right)^2},\psi(f_1,f_2)=e^{-\left(\frac{|f_1-f_2|}{h}\right)^2}$ ,$r$ 和 $h$ 是到附近点的(特征)距离平均值。这也就是所谓的双边插值(bilateral interpolation),即同时考虑空间相似度和特征相似度的插值方式。
实现层间连接的方式可以是对先前所有层的 $\widetilde{f}_i$ 进行插值和连接,即密集连接,这和特征提取单元是一样的。但是这样做意味着第 $\ell$ 层会有 $\ell C$ 个特征,导致扩展性差、优化困难。因此论文采用了残差跳跃连接,每个级别只需要和上一个级别的特征相连,这在下图中展现得很清楚。

实施细节
迭代提取 patch
训练
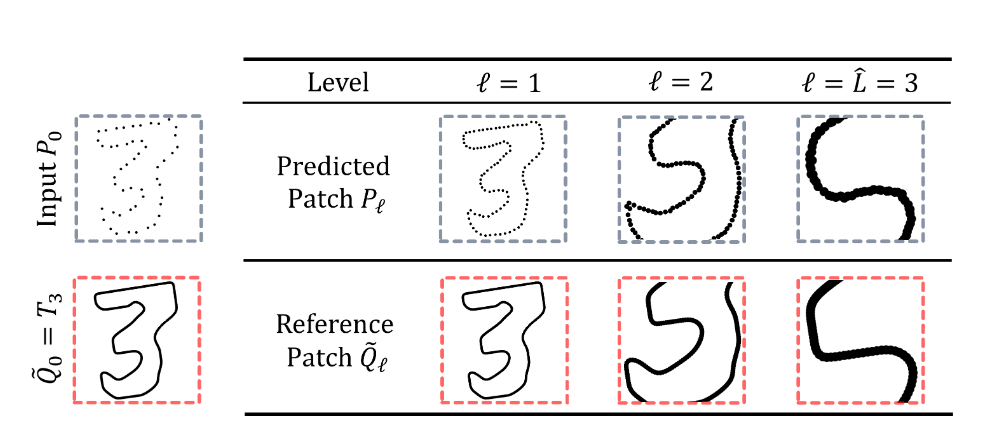
$P_{\hat{L}},Q_{\hat{L}}$ 分别表示预测和参考 patch ,$T_{\hat{L}}$ 则表示该分辨率下的整体参考点云。在渐进式上采样过程中,则会有一系列预测和参考 patch ,记作 $P_{\ell},Q_{\ell}$ ,其中 $\ell=1\dots\hat{L}-1$ 。
具体来说,$\ell$ 层的输入是通过对 $P_{\ell-1}$ 中的随机点 $p_{\ell-1}’$ 执行 KNN 搜索得到的,其中 $k=N$ ,为 patch 的大小。而 $\widetilde{Q}_{\ell}$ 应与 $P_{\ell}$ 的空间范围相匹配,同时具有更高的分辨率,因此 $Q_{\ell}$ 可以通过在 $Q_{\ell-1}$ 中执行 KNN 得到,并且查询点仍为 $p_{\ell-1}’$ 。此时 $k=2^{\hat{L}-\ell+1}N$ (这里符号表示和原文不同,因为 * 有转义字符的含义,网页里似乎优先级高于公式)。
关于这个结论,可以先考虑第 $1$ 层:我们希望将第一层的 $N$ 个点上采样为 $2^{\hat{L}}$ 个点,因此在参考点云中,需要采样 $2^{\hat{L}-0}=2^{\hat{L}}$ 个点;而点云被上采样 $\ell-1$ 次之后,到达了 $\ell$ 层,此时需要在参考点云中采样的点数变为 $2^{\hat{L}-(\ell-1)}=2^{\hat{L}-\ell+1}$ 。如下图所示,需要注意的是 $Q_{\ell}$ 的分辨率是不随 $\ell$ 变化的,仅仅是空间范围变化而已,换言之,$\left|P_{\ell}\right|/\left|Q_{\ell}\right|$ 等于 $P_{\ell}$ 和基准点云的分辨率之比,随着上采样次数增加,$P_{\ell}$ 的分辨率增大,patch 点数不变的情况下, $Q_{\ell}$ 的点数随之减少。
推理
推理阶段和训练主要有两个不同:
- 对于每个级别,提取 $H$ 个有重叠的输入 patches 以确保覆盖整个点集。patch 的中心点通过最远点采样获得;
- 由于有重叠,上采样后的点数实际上大于 $2\left|P_{\ell-1} \right|$ ,因此对 $P_{\ell}$ 进行最远点采样,使其点数为上一层的两倍。这同样有助于上采样结果均匀分布。
损失函数
考虑到计算速度,论文采用了欧氏距离进行 patch 提取,但这可能导致 $P_{\ell}$ 和 $Q_{\ell}$ 的边缘产生错位问题,也就是空间范围不一致。为了降低这些不匹配点带来的噪声,论文提出了改进的 Chamfer 距离:
相比于之前在 PU-Net 里所介绍的 CD 距离,其实就差了一个 $\xi$ 函数。其中 $\delta$ 设置为平均最近邻距离的倍数,以便动态调整到不同尺度的 patch (至于为什么是倍数,可能因为尺度较大时这个条件可以被适当放宽?)。
四、总结
论文所做的主要工作包括:
- 提出了新的特征提取和特征扩展单元,其中特征提取部分在特征空间上定义了邻域,无需下采样,避免了特征连接需要点对应搜索的问题,并通过密集连接复用信息;特征扩展部分采用了附加变量的方式,使用共享的 MLP ,起到控制参数量、促使点均匀分布的作用;
- 在不同层之间利用双边插值进行残差连接,同时考虑特征距离和空间距离;
- 随着不断上采样、感受野缩小的同时,缩小了 patch 的空间跨度,即自适应 patch 。这使得网络可以端到端地训练;